The Matrix (Higher Order) Kalman Filter

←Back ←

This document gives the skeleton of the derivation of a matrix (higher order) Kalman filter.  The math follows in the same was as the scalar case, but uses matrix variables.  Rigorous derivations are given in the references.

Matrix Variables

The matrix problem proceeds just as the scalar problem, but all of the variables are now matrices.   The system has p inputs, n state variables and m outputs.

variable  Scalar   Matrix   Matrix size 
state xj xj n by 1
input uj uj p by 1
output zj zj m by 1
state gain a A n by n
input gain b B n by p
output gain h Hj m by n
process noise wj wj n by 1
process noise covariance Q Q n by n
measurement noise vj vj m by 1
measurement noise covariance R R m by m
a priori covariance n by n
a posteriori covariance n by n
Kalman Filter Gain kj Kj n by m

The solution proceeds as did the scalar case.  Only major results will be presented here, the intermediate results are not discussed, but can be determined by analogy with the derivation of the scalar kalman filter.

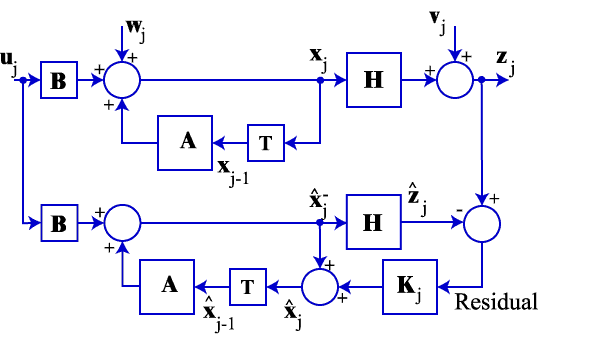
A discrete time system with process noise w and measurement noise v is defined by:

   Equation 1

The corresponding block diagram is shown below

The block diagram for a Kalman filter is given by:

 

The predictor equation is given by

     Equation 2

The corrector equation is given by

     Equation 3

The a priori and a posteriori covariances are given by 

    

where the superscript T denotes the matrix transpose.

To find the best value for the filter gain, Kj, differentiate the a posteriori covariance and set it to zero:

The Kalman filter gain is obtained after much algebra and is given by

     Equation 4

The recursive form of the a priori covariance is given by:

    Equation 5

The recursive calculation of the a posteriori covariance is given by:

    Equation 6

Equations 2 through 6 give the Kalman filter algorithm.  The other equations are only necessary for the derivation of the gain and covariances.

 

← Back←