The SCAM program cannot simply read a schematic diagram so we need to develop a method for representing a circuit textually. This can be done using a device called a netlist that defines the interconnection between circuit elements. If you have used SPICE (Simulation Program with Integrated Circuit Emphasis) this is a familiar concept. A good review is given by Jan Van Der Spiegel at the University of Pennsylvania. The process is easily demonstrated by example.
Let us use SCAM to define the circuit below:

We start by defining the nodes. The only restriction here is that the nodes must be labeled such that ground is node 0, and the other nodes are named consecutively starting at 1. The choice of which number to assign to which node is entirely arbitrary.

SCAM requires a text file with one line for each component in the circuit. This circuit has 4 components (3 resistors and 1voltage source), and will require 6 lines to define it. Each type of component has its own format for its corresponding lines in a file. These are shown below. The labels N1, N2, etc... correspond to the nodes in the circuit.
| Component Type | Symbol | SCAM Description |
| Resistor |  |
R1 N1 N2 1000
|
| Capacitor |  |
C1 N1 N2 1E-6
|
| Inductor | L1 N1 N2 1E-3
|
|
| Voltage Source |  |
V1 N1 N2 12
|
| Current Source |  |
I1 N1 N2 1
|
| Op Amp |  |
O1 N1 N2 N3
|
Let's define the current through the voltage source to give a final circuit diagram:

The netlist file is:
V1 1 0 12 R1 1 2 1000 R2 2 0 2000 R3 2 0 2000 |
Example 1: Voltages
Let's use the circuit we have been examining
We will create a text file containing the netlist:
and save it in the directory seen by MATLAB. I edited such a file (using the MATLAB editor) and saved it in my SCAM directory as Example1.cir. If you are running MATLAB, you should see the file if you use the dir command:
>> dir . .. scam.asv scam.m Example1.cirTo run the program, assign the filename of the circuit to be analyzed to the variable fname, and then call the program. The output from the MATLAB window is shown below:
>> fname='Example1.cir'; >> scam Started -- please be patient. Done! Elapsed time = 0.651 seconds. Netlist V1 1 0 12 R1 1 2 1000 R2 2 0 2000 R3 2 0 2000 Solved variables: [ v_1] [ v_2] [ I_V1]The netlist is displayed, followed by the unknown variables whose solution is determined. Let's look at the value of v_2 (the voltage at node 2):
>> v_2
v_2 = 1/(R2*R3+R1*R3+R1*R2)*R2*R3*V1or I_V1 (the current through the voltage source)
>> I_V1
I_V1 = (-R3-R2)/(R2*R3+R1*R3+R1*R2)*V1In addition to the unknowns, several other variables are created in the workspace (this is why the SCAM program is a script instead of a function). The important variables created, in addition to the unknowns, are a value corresponding to each of the elements. We can examine the value of any element, for example V1 or R2
>> V1
V1 = 12
>> R1
R1 = 1000We can use these values to get numeric values for the unknowns:
>> eval(v_2)
ans = 6
>> eval(I_V1)
ans = -0.0060which shows that the voltage at node 2 is 6 volts, and the current through V1 is 6 mA.
Example 2: Currents
What happens if we are interested in the current through R2 instead of just node voltages, from node 2 to node 0. We know that the current through R2 is just the voltage drop across R2, divided by the value of the resistance. We can do the solution either symbolically or numerically.
>> v_2/R2
ans = 1/2000/(R2*R3+R1*R3+R1*R2)*R2*R3*V1
>> eval(ans)
ans = 0.0030The current through R1, from node 1 to node 2, is just the voltage across R1 divided by its value.
>> (v_1-v_2)/R1
ans = 1/1000*V1-1/1000/(R2*R3+R1*R3+R1*R2)*R2*R3*V1
>> eval(ans)
ans = 0.0060Other quantities can be similarly determined. For example the ratio of v_2 to V1:
>> v_2/V1
ans = 1/12/(R2*R3+R1*R3+R1*R2)*R2*R3*V1
>> eval(ans)
ans = 0.5000
Example 3: Generating MNA Equations
The SCAM program also defines the A, X and Z matrices from the MNA method. (Note that the SCAM program uses uppercase variables for X and Z).
>> A
A = [ 1/R1, -1/R1, 1]
[ -1/R1, 1/R1+1/R2+1/R3, 0]
[ 1, 0, 0]
>> X
X = [ v_1]
[ v_2]
[ I_V1]
>> Z
Z = [ 0]
[ 0]
[ V1]We can use these variables to recreate the circuit equations. To get the left side of the equations we just multiply A*X:
>> A*X ans = [ 1/R1*v_1-1/R1*v_2+I_V1] [ -1/R1*v_1+(1/R1+1/R2+1/R3)*v_2] [ v_1]or, in a slightly easier to read form:
>> pretty(A*X) [ v_1 v_2 ] [ --- - --- + I_V1 ] [ R1 R1 ] [ ] [ v_1 / 1 1 1 \ ] [- --- + |---- + ---- + ----| v_2] [ R1 \ R1 R2 R3 / ] [ ] [ v_1 ]The left side of the equation is given by Z:
Z = [ 0] [ 0] [ V1]Using the information above, we can get any of the MNA equations. To get the equations for node 2, simply take the 2nd row of the right and left sides of the equations:
Example 4: A More Complex Circuit
We can also apply the program to more complex circuits, such as the following (Example 3 from the MNA Examples page with values given to each component) (with nodes already labeled, and the currents through the voltage sources also labeled for clarity):
The netlist for this circuit is given by
I entered this into a file and named it Example4.cir. To analyze the circuit we proceed as before, by setting the fname variable, and starting the program:
>> fname='Example4.cir'; >> scam Started -- please be patient. Done! Elapsed time = 2.544 seconds. Netlist Vg 1 0 4 Vx 3 2 6 R1 1 2 1 R2 2 0 4 R3 3 0 2 It 1 2 1 Solved variables: [ v_1] [ v_2] [ v_3] [ I_Vg] [ I_Vx]We can solve for the voltage at node 2 either symbolically or numerically:
>> v_2 v_2 = R2*(It*R1*R3+Vg*R3-Vx*R1)/(R2*R3+R1*R3+R1*R2) >> eval(v_2) ans = 1.1429We can find the current through R1 (symbolically or numerically):
>> (v_1-v_2)/R1 ans = Vg-R2*(It*R1*R3+Vg*R3-Vx*R1)/(R2*R3+R1*R3+R1*R2) >> eval(ans) ans = 2.8571We can find the MNA equation for node 2:
>> q=A*X q = [ 1/R1*v_1-1/R1*v_2+I_Vg] [ -1/R1*v_1+(1/R1+1/R2)*v_2-I_Vx] [ 1/R3*v_3+I_Vx] [ v_1] [ -v_2+v_3] >> pretty(q(2)) v_1 / 1 1 \ - --- + |---- + ----| v_2 - I_Vx R1 \ R1 R2 / >> Z(2) ans = Itor, in a cleaner format
Example 5: Op Amps w/ resistors
The next example shows an op-amp with 2 resistors in the standard inverting configuration along with its netlist (Example5.cir).
Circuit Netlist

Since we don't have values for the components in the circuit, they are declared to be "Symbolic". We can now solve this circuit to determine the gain between Vin and node 2.
>> fname='Example5.cir'; >> scam Started -- please be patient. Done! Elapsed time = 1.633 seconds. Netlist Vin 3 0 Symbolic R1 1 3 Symbolic R2 2 1 Symbolic OAmp 0 1 2 Solved variables: [ v_1] [ v_2] [ v_3] [ I_Vin] [ I_OAmp] >> v_2/Vin ans = -1/R1*R2Some notes on this circuit:
- If a value is not given for an element, the value can be declared symbolic (as above). However this is not necessary, the user must simply ensure that the value is not a number -- so instead of "Symbolic", the value of R1 could have been "zyx" or even left blank.
- Because of the way we have used MNA to handle op-amps, the circuit above would give the exact same results even if the input terminals were switched. In practice this would not work. It is the responsibility of the user to make sure negative feedback exists.
Example 6: Converting the symbolic transfer function to a MATLAB object.
Often we would like to take our results and use them in MATLAB for other calculations. this is especially true when working with transfer functions. The example below shows how this can be accomplished. This circuit is from the MNA with Capacitors and Inductors page with values given to each component, with nodes already labeled, and the currents through the voltage sources also labeled for clarity. The netlist is called Example6.cir.
Circuit Netlist
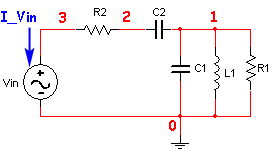
Now let's solve and get the transfer function symbolically
>> fname='Example6.cir'; >> scam Started -- please be patient. Done! Elapsed time = 1.583 seconds. Netlist Vin 3 0 Symbolic R2 3 2 1000 R1 1 0 1000 C1 1 0 1E-6 C2 2 1 10E-6 L1 1 0 0.001 Solved variables: [ v_1] [ v_2] [ v_3] [ I_Vin] >> v_2/Vin %Find transfer function between input and node 2 ans = (s*L1+s^2*C1*R1*L1+s^2*C2*R1*L1+R1)/(s*L1+s^2*L1*C2*R2+s^2*C1*R1*L1+s^3*C1*R1*L1*C2*R2+s^2*C2*R1*L1+R1+R1*s*C2*R2) >> collect(ans) %Collect similar terms ans = ((C2*R1*L1+C1*R1*L1)*s^2+s*L1+R1)/(s^3*C1*R1*L1*C2*R2+(C2*R1*L1+L1*C2*R2+C1*R1*L1)*s^2+(L1+R1*C2*R2)*s+R1) >> pretty(ans) %Pretty print it 2 / 3 ((C2 R1 L1 + C1 R1 L1) s + s L1 + R1) / (s C1 R1 L1 C2 R2 / 2 + (C2 R1 L1 + L1 C2 R2 + C1 R1 L1) s + (L1 + R1 C2 R2) s + R1)
We can also get a numerical transfer function
>> eval(v_2/Vin) ans = (1/1000*s+11/1000000*s^2+1000)/(10001/1000*s+21/1000000*s^2+1/100000000*s^3+1000)
While this answer is correct, it is not in a very convenient form, and we can't do any actual simulation with it. However we can easily convert the expression to a MATLAB transfer function object. First we separate out the numerator and denominator, and then convert them to MATLAB polynomials.
>> [n,d]=numden(eval(v_2/Vin))
n = 100000*s+1100*s^2+100000000000
d = 1000100000*s+2100*s^2+s^3+100000000000
>> mySys=tf(sym2poly(n),sym2poly(d))
Transfer function:
1100 s^2 + 100000 s + 1e011
--------------------------------
s^3 + 2100 s^2 + 1e009 s + 1e011
We are now free to perform any of the MATLAB function relating to polynomials. Shown below are a step response and a Bode plot.
| Step Response | Bode Plot |
| >> step(mySys) | >> bode(mySys) |
 |
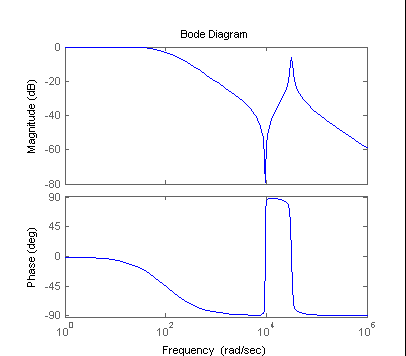 |
Example 7: Finding the current in a wire
Now consider the case of finding the current through a wire. In particular, consider the previous circuit:
We would like to find the current shown. How do we do this. One way would be to find each current into and out of node 1 and solve for the unknown current. Another way is to introduce a voltage source of zero volts (i.e., a short circuit), and its concomitant node. The netlist is Example7.cir.
Circuit Netlist
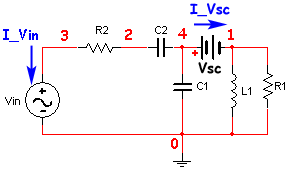
This voltage source has no effect on the circuit, but forces the computation of the current I_Vsc.
>> fname='Example7.cir'; >> scam Started -- please be patient. Done! Elapsed time = 3.014 seconds. Netlist Vin 3 0 Symbolic R2 3 2 1000 R1 1 0 1000 C1 4 0 1E-6 C2 2 4 10E-6 L1 1 0 0.001 Vsc 4 1 0 Solved variables: [ v_1] [ v_2] [ v_3] [ v_4] [ I_Vin] [ I_Vsc] >> eval(I_Vsc) ans = -1/100000*(-1/1000*s-1000)*s*Vin/(10001/1000*s+21/1000000*s^2+1/100000000*s^3+1000) >> simplify(ans) ans = (s+1000000)*s*Vin/(1000100000*s+2100*s^2+s^3+100000000000) >> pretty(ans) (s + 1000000) s Vin ------------------------------------------ 2 3 1000100000 s + 2100 s + s + 100000000000




